在一片广袤的森林里,有一只名叫乌鸦的黑鸟,乌鸦是出了名的聪明。然而,它却有个奇特的习惯,收集各色各样的石头。每当找到一颗特别或是形状奇特的石头,乌鸦就会兴高采烈地将其收入自己的巢中。
有一天,乌鸦在森林的另一角落发现了一个浅浅小水塘。塘底躺着许多五彩斑斓的石头,每一种都闪耀着诱人的光芒。乌鸦见状,灵光一动。它叼起一颗石头,飞到了水塘边。乌鸦用石头去击溅起水花,然后迅速张开嘴巴,欣赏四溅的水珠,乌鸦希望看到的水花尽量大,但是乌鸦不希望石子溅起水花后有石子露出水面,这意味着乌鸦使用的石头体积要尽量大,且不能超过水面。
由于乌鸦很聪明但又没有那么聪明,为了简化问题,我们把石子认为是长方体,池塘表面认为是矩形,矩形大小为 m * n,对池塘建立直角坐标系,池塘四周都是竖直的,并测得了每个单位方格的深度(深度表示池塘表面到池塘底部的距离)。当石子沉入水中时,石子会一直下沉直到碰到池底。沉底时,石子的顶面会和池塘的表面平行,石子的边缘会和网格对齐。石子排开了一部分水,这会使池塘的水位上升(排开水的体积等于石头的体积)。池塘四周的墙面足够高,所以水不会溅出来。
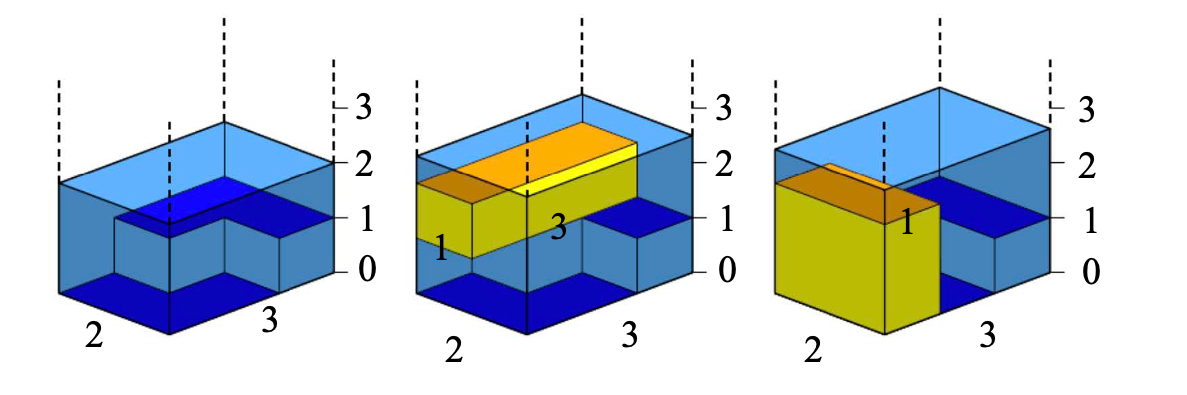
例如,在下图中,左边的图表示池塘的形态,中间的图表示一种体积为 3 的放置方法,右边的图表示一种体积为 4 的放置方法。这也是能够藏下的最大体积。注意,如果右边的图的石子再变高 1 单位,它的顶面就能被看到了,因为此时它的顶面和水面一样高,注意,石子与水面一样高也是不可行的。
乌鸦只想丢一次石头,它想知道在不看到石子情况下,能够丢下池塘的石子最大体积是多少?你能告诉它吗?