美食家小明最近迷上了吃包子,于是上天降下来了 n 桶神奇的包子,编号为 1,2,.......,n,每桶包子的数量可以认为是无限的。
小明会从第 1 桶包子走到第 n 桶,这样总共走 m 趟,每一趟,都从第 1 桶走到第 n 桶。当他走到一桶包子前时,他就会在这里吃一次包子,有一件奇怪的事是,当小明吃一次包子时,所有包子桶中的包子都会减少。同时,小明发现了一个问题,就是他手太短了,只能拿到距离桶口 < x 范围内的包子,如果包子减少太多会导致他够不到包子。
一开始,第 i 桶包子的深度(桶口到包子的距离)为 w_i,每当小明吃一次包子,所有桶中包子的深度都会增加,其中,第 i 桶包子的深度增加 a_i,注意,小明吃包子可以认为的瞬间的, 如果一开始够得着,但吃完后够不着,也视为一次成功的吃包子,包子深度也一样会增加。
小明想着知道他可以吃到多少次包子。
第一行三个正整数 n,m,x,表示有 n 桶包子,小明会走总共 m 趟,能够到桶口与包子距离不超过 x 的包子。
第二行,n 个正整数,第 i 个数为第 i 桶包子的初始深度 w_i。
第三行,n 个正整数,第 i 个数为小明吃包子时第 i 桶包子增加的深度 a_i。
【样例解释】
第一趟:
小明走到第 1 桶包子处,成功吃了 1 次包子,各桶深度变为 {10,10,10};
小明走到第 2 桶包子处,成功吃了 1 次包子,各桶深度变为 {12,11,13};
小明走到第 3 桶包子处,成功吃了 1 次包子,各桶深度变为 {14,12,16}。
第二趟:
小明走到第 1 桶包子处,成功吃了 1 次包子,各桶深度变为 {16,13,19};
小明走到第 2 桶包子处,成功吃了 1 次包子,各桶深度变为 {18,14,22};
小明走到第 3 桶包子处,够不到包子,各桶深度仍为 {18,14,22}。
第三趟:
小明走到第 1 桶包子处,够不到包子,各桶深度仍为{18,14,22};
小明走到第 2 桶包子处,成功吃了 1 次包子,各桶深度变为 {20,15,25};
小明走到第 3 桶包子处,够不到包子,各桶深度仍为{20,15,25}。
第四趟:
小明走到第 1 桶包子处,够不到包子,各桶深度仍为{20,15,25};
小明走到第 2 桶包子处,成功吃了 1 次包子,各桶深度变为{22,16,28};
小明走到第 3 桶包子处,够不到包子,各桶深度仍为{22,16,28}。
因此小明一共吃了 7 次包子。
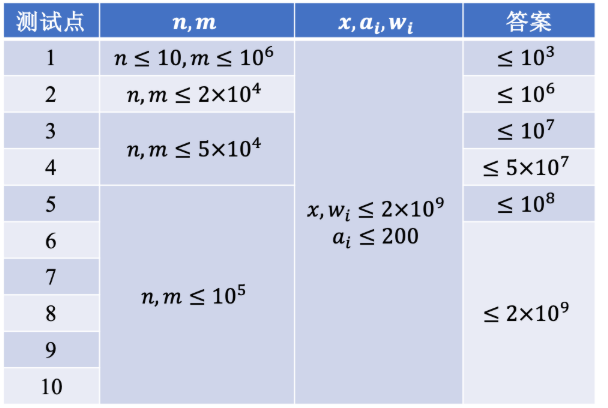
【数据范围】